The connection between visual learning and bar model drawing techniques

Wiki Article

Exploring Bar Design Drawing Techniques: A Comprehensive Overview to Picturing Math Concepts

Bar version attracting techniques work as a useful source for both teachers and trainees in visualizing mathematical concepts. These designs simplify complicated numerical relationships, aiding in the comprehension of addition, reproduction, division, and subtraction. This overview lays out efficient methods for applying bar designs, fostering active interaction and real-world links. As viewers explore the sensible applications and teaching pointers, they will certainly uncover just how these strategies can change their technique to mathematics.

Recognizing the Basics of Bar Design Drawing

Bar model attracting works as an effective visual tool in maths, helping with the understanding of analytical techniques and numerical connections. This strategy involves representing numbers and their connections via rectangle-shaped bars, making it easier to picture operations such as enhancement, reproduction, reduction, and division. Each bar's length corresponds to a particular value, enabling learners to contrast amounts and understand percentages plainly.

To develop a bar design, one begins by identifying the problem's essential components, commonly damaging it down into components that can be visually represented. In a simple enhancement trouble, two bars can be attracted, with their lengths standing for the addends. The mixed size illustrates the amount. On top of that, bar versions can be adjusted for much more complex problems, including portions and proportions, by adjusting the bars as necessary. Understanding these fundamentals lays a solid structure for reliable analytic and deeper mathematical understanding.

Advantages of Using Bar Designs in Mathematics

Using bar designs in mathematics uses numerous benefits that boost discovering and comprehension. These graphes help trainees in grasping intricate concepts by breaking them down into workable components. Bar designs offer a clear framework for illustrating connections between numbers, making abstract concepts much more concrete. They advertise a much deeper understanding of mathematical operations and help with analytic by enabling learners to envision the information they are collaborating with.

Additionally, bar versions support the development of essential thinking skills, as trainees must assess and analyze the aesthetic details to draw final thoughts. This method motivates active interaction with the material, enhancing retention and proficiency of mathematical concepts. By cultivating a solid foundation in aesthetic proficiency, bar versions equip students to come close to numerous mathematical obstacles with self-confidence. Overall, the combination of bar models right into maths education and learning shows helpful in cultivating both comprehension and analytical abilities amongst pupils.

Using Bar Models to Addition and Reduction

Bar versions act as a reliable tool for aesthetically standing for addition and subtraction problems. By showing the relationship in between numbers, they enhance understanding and help with problem-solving. Additionally, real-life applications of these designs can help learners comprehend mathematical concepts in functional contexts.

Standing For Enhancement Visually

When trainees run into addition and subtraction issues, aesthetic help can greatly improve their understanding of these operations. Bar versions serve as reliable tools for representing addition. By separating a rectangular shape into sectors that correspond to the numbers involved, pupils can picture the relationship between the quantities. If a student requires to include 3 and 5, they can develop a bar split right into 2 areas: one section standing for 3 and the various other representing 5. This clear depiction not just simplifies the enhancement procedure yet likewise reinforces the idea of combining quantities. As students control these visual aids, they establish a much deeper understanding of addition, resulting in enhanced analytic skills and higher confidence in their mathematical capacities.

Subtraction With Bar Models

Subtraction is frequently perceived as an extra intricate procedure than enhancement, bar versions can effectively clarify this procedure for pupils. By aesthetically standing for the quantities involved, pupils can much better comprehend just how numbers relate to one another. In a bar version for reduction, one bar stands for the overall, while another suggests the quantity being deducted. This aesthetic difference aids pupils grasp the idea of "eliminating." As an example, if a bar reveals 10 devices, and an additional bar standing for 4 devices is eliminated, trainees can quickly see that 6 systems stay. This method not only fosters understanding of subtraction however additionally help in creating analytic abilities, enabling pupils to picture their mathematical thinking and boost their total understanding of mathematical ideas.

Real-Life Application Instances

Understanding reduction with bar models lays a foundation for using these methods in real-life situations. In various contexts, such as budgeting or shopping, people can picture exactly how much money continues to be after expenditures. As an example, if a person has $50 and spends $20, a bar version can stand for the total amount and the invested part, illustrating that $30 is left. Additionally, moms and dads can make use of bar models to help children recognize the number of even more products need to be included in finish a set, such as having three apples and requiring five. This graph simplifies complicated troubles, helping with understanding and retention. Inevitably, bar designs function as reliable devices in day-to-day decision-making, boosting mathematical understanding in sensible situations.

Visualizing Multiplication and Department With Bar Designs

In exploring the application of bar designs for reproduction and department, it is vital to understand their fundamental concepts. Constructing reproduction designs enables students to imagine partnerships between numbers, while efficient division strategies can be highlighted with these visual aids. This strategy boosts understanding and problem-solving skills in mathematics.

Understanding Bar Versions

Bar versions act as a powerful visual device for highlighting the ideas of multiplication and department. They enable learners to represent mathematical partnerships in a structured layout, promoting a deeper understanding of these procedures. In reproduction, bar models show groups of equivalent dimension, enabling individuals to visualize the overall quantity when combining these teams. On the other hand, in department, bar versions assist portray just how an overall is divided right into smaller sized, equivalent components, clearing up the concept of partitioning. By utilizing these visual help, students can comprehend the underlying principles of multiplication and division more properly. This strategy not just boosts understanding yet likewise supports problem-solving abilities, making bar models an indispensable possession in mathematical education.

Building Multiplication Versions

Creating multiplication designs utilizing bar diagrams provides a clear technique for imagining the process of reproduction. These models make it possible for learners to represent multiplication as groups of equal components, making abstract principles extra More Help concrete. To illustrate (3 times 4), a trainee can draw one bar separated into 3 equal segments, each standing for 4 systems. Additionally, creating a 2nd bar with the exact same size reinforces the understanding of duplicated enhancement, as each segment corresponds to one team. This graph not only help in grasping multiplication but also enhances analytical skills. By using bar designs, trainees can much better comprehend partnerships in between numbers and establish a robust structure for extra intricate mathematical principles, leading to raised confidence in their capacities.

Picturing Division Approaches

While multiplication typically gets the spotlight in early math education and learning, division is just as important and can be efficiently envisioned using bar versions. Bar versions provide a clear aesthetic representation of department troubles, damaging down the process into workable components. For circumstances, when dividing a total right into equal groups, students can draw a long bar to stand for the whole and after that segment it into smaller sized bars that indicate each team. This approach not just illustrates the principle of equivalent sharing but also enhances the connection between reproduction and division. By utilizing bar versions, learners can better understand division as a process of dividing, aiding to solidify their understanding of this basic mathematical procedure.

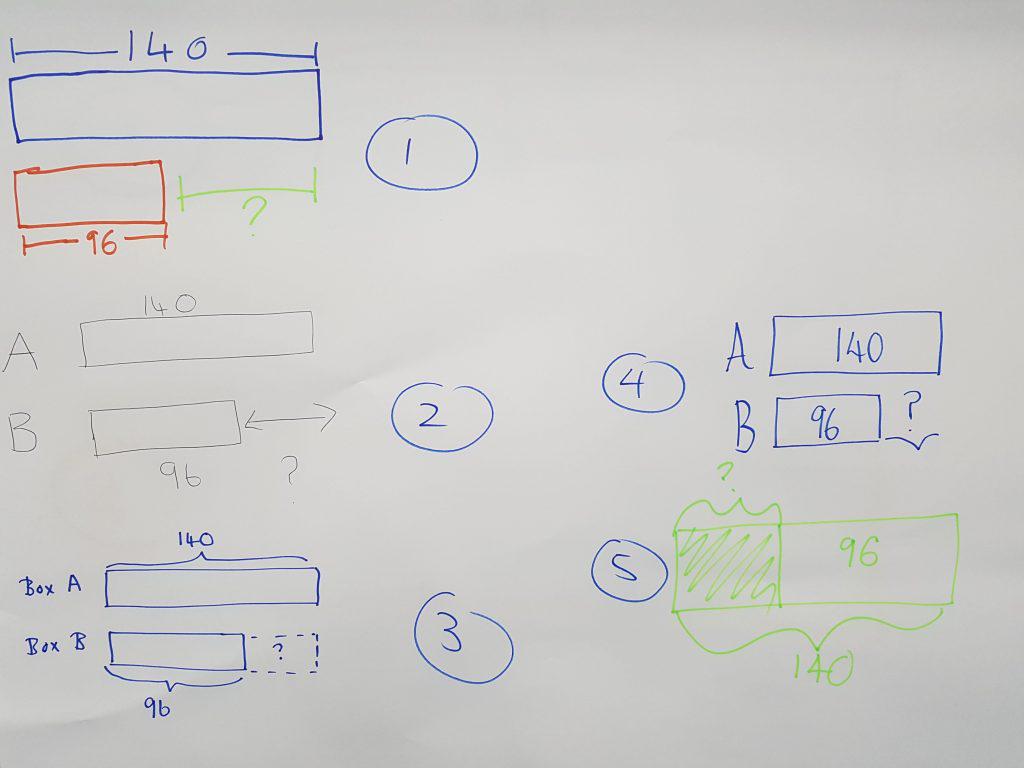
Fixing Word Troubles Using Bar Model Techniques

How can aesthetic depictions enhance the understanding of word issues? Bar model methods supply a powerful tool for trainees to damage down intricate scenarios right into manageable parts. By equating words into aesthetic bars, students can determine relationships in between quantities and operations more easily. Each bar represents a details value, allowing trainees to see how different aspects of the problem connect.

For example, in a trouble involving addition and reduction, trainees can draw different bars for each quantity and then adjust them to find the service. This procedure not like this only makes clear the issue however also promotes a deeper conceptual understanding. Moreover, bar versions can be adjusted for different sorts of word troubles, making them functional throughout different mathematical subjects. Eventually, utilizing bar models can substantially improve students' problem-solving skills by giving a clear visual pathway to come to the proper answer.

Integrating Bar Versions in Different Mathematics Topics

Bar designs can be flawlessly integrated into different mathematics subjects, boosting pupils' understanding of concepts beyond standard math. In algebra, these aesthetic tools aid in standing for inequalities and equations, enabling learners to envision partnerships in between variables. When dealing with geometry, bar models can show the homes of forms and spatial thinking, assisting students grasp ideas like area and perimeter effectively. In stats, bar versions promote the interpretation of information sets, allowing students to contrast amounts and acknowledge trends visually. Furthermore, integrating bar designs within dimension topics aids in understanding devices and conversions by offering a concrete depiction of amounts. By employing bar versions throughout various mathematical areas, instructors can promote a much deeper understanding of intricate ideas, therefore boosting analytical skills and advertising critical reasoning (bar model drawing techniques). This adaptability shows the utility of bar versions as a foundational device for students in their mathematical trip

Tips for Teaching Bar Designs Effectively

Integrating bar versions into training techniques requires thoughtful approaches to optimize their performance. Educators needs to begin by presenting bar versions with basic, relatable instances that students can conveniently grasp. This helps to construct self-confidence and experience with the idea. Progressively boosting the intricacy of issues enables students to use their abilities considerably. Furthermore, instructors must urge pupils to create their very own bar designs, advertising energetic interaction and possession of their learning.


Integrating collaborative activities can additionally boost understanding, as pupils review and resolve issues in teams. Constant comments is necessary; teachers should give positive discourse on trainees' bar version depictions to direct renovation. Connecting bar versions to real-life situations strengthens their significance, helping pupils see the useful applications of their mathematical abilities. By executing these methods, teachers can effectively harness the power of bar designs in their mathematics instruction.

Frequently Asked Questions

Can Disallow Designs Be Used in Various Other Topics Besides Math?

Bar models can indeed be made use of in numerous subjects beyond math. They successfully illustrate concepts in scientific research, social studies, and language arts, aiding to aesthetically stand for connections, procedures, and concepts for boosted understanding throughout disciplines.

What Age Is Ideal Fit for Learning Bar Designs?

Bar designs are best fit for kids ages 7 to 12, as they develop concrete thinking abilities during this period (bar model drawing techniques). At this age, students can properly understand abstract principles via aesthetic representation and analytic techniques

Exist Digital Equipment for Creating Bar Versions?

Yes, numerous digital devices exist for creating bar versions, including academic software program and online platforms. These tools assist pupils envision mathematical concepts effectively, improving their understanding and engagement in finding out through dynamic and interactive representations.

Just How Can I Assess Trainee Recognizing of Bar Models?

Examining student understanding of bar versions can entail quizzes, empirical analyses, and seminar. this page Teachers may additionally analyze students' completed models and their capability to discuss their thinking, ensuring a comprehensive examination of comprehension.

What Are Usual Mistakes When Using Bar Models?

Typical blunders when utilizing bar versions include misrepresenting quantities, falling short to precisely classify bars, confusing addition and reduction, ignoring to use consistent ranges, and ignoring the significance of clear visual splitting up in between various elements.

In enhancement, bar versions can be adapted for much more intricate problems, including fractions and proportions, by changing the bars accordingly. Reduction is often regarded as a much more intricate procedure than enhancement, bar versions can efficiently clarify this procedure for pupils. In a bar version for reduction, one bar stands for the total, while an additional indicates the quantity being subtracted. If a bar reveals 10 units, and one more bar representing 4 systems is gotten rid of, trainees can quickly see that 6 devices remain. When splitting a total amount into equal teams, students can draw a lengthy bar to represent the whole and after that sector it into smaller sized bars that suggest each group.

Report this wiki page